Umesh Chandra

Binary Tree, The word binary itself says it is a base-2 numeral number system. Similarly Tree, It has branches, roots etc. But in the language of programming we call branches of a tree as Nodes. A tree can have ‘n’ number of branches, But Binary Tree is a tree which has at most 2 children for a Node. So, the Nodes are defined as Left Node and Right Node. The top most node is called Root, and the bottom most nodes are called as Leaf Nodes.

We have another terms Height and Depth of a binary tree,

Height of a Binary Tree – The number of edges from the deepest node in the tree to the root node.

Depth of a Binary Tree – The number of edges from a node in the tree to the root node.

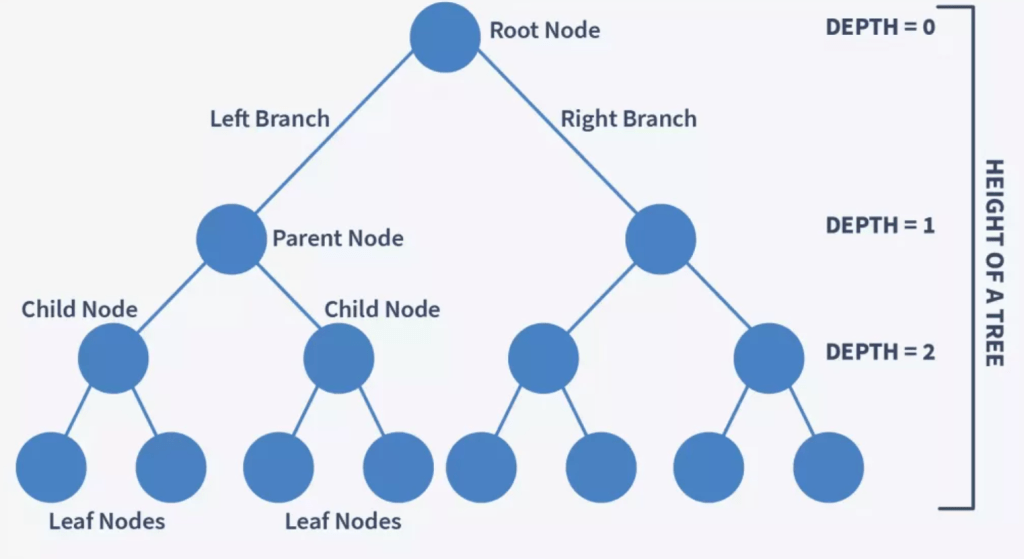
Properties of a Binary Tree

The height of a perfect binary tree, where there are n nodes (more on them later), is given by -log n. This is due to the fact that there can only ever be two child nodes for a given node in a binary tree. This further leads us to the argument that the number of nodes at each level or height of a binary tree will be almost equal to half that of the nodes present in the level above. Simply put, in a binary tree, there are approximately twice as many nodes at each level as there were at the level before it.